| |
4-3 MD5 訊息摘要
內容:
『訊息摘要』(Message Digest)是由 Ron Rivest(RSA 中的 “R”)在 MIT 所發展的一系列雜湊演算法,其中較著名的有 MD2(RFC 1319)、MD4(RFC 1320) 與 MD5(RFC 1321)。MD2 主要是以 8 個位元為單位的計算方式,複雜度較弱,一般都將該演算法崁入於數位晶片上,如 IC 卡。MD4 與 MD5 都是針對 32 位元 CPU 所設計的;MD5 是由 MD4 改良得來,主要為了增加複雜度,就目前而言,MD5 早已凌駕 MD4 之上。
4-3-1 MD5 運作原理
MD5 是將不定長度的訊息,演算成一個 128 個位元長的訊息摘要(或稱雜湊碼);計算方式是屬於串接式的區塊演算法,如圖 4-3 所示。處理步驟如下:
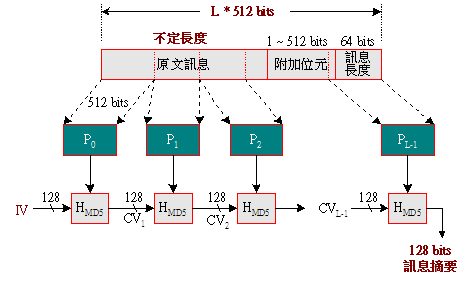
圖 4-3 利用 MD5 產生訊息摘要
-
步驟 1:加上一些附加位元(Padding Bits),使得訊息長度除以512餘數為448(448 mod 512)。如果訊息的長度剛好滿足448 mod 512時,仍必須加入 512 bits 的附加位元。所附加位元的資料除第一個位元為1,其餘皆為0。
-
步驟 2:加上 64 bits 長度欄位,其內容表示原訊息的長度,以位元為單位。如果長度超過 264 個位元,則只取最低 64 位元的資料;亦即 mod 264。
-
步驟 3:以每 512 bits 為單位,將訊息分割為L個區塊 {P0, P1, .., Pq, …, PL-1}。
-
步驟 4:將第一區塊(P0)與起始向量(Initial Vector, IV,128 bits)輸入到 MD5 演算法中,輸出為 CV1(128 bits);CV1 則作為下一個區塊P1的輸入向量,依此類推。
-
步驟 5:最後區塊(PL-1)與前一個 CVL-1 經由 MD5 演算後的輸出值,即為該訊息的訊息摘要(或稱雜湊值,128 bits)。
起始向量(IV)是一個重要的參數,每次演算時加入不同的 IV 值,可以增加破解的困難度。一般來講,IV 值只要在雙方協商時,以明文傳送即可(亦可加入於原訊息中一起加密)。
4-3-2 MD5 演算法
接下來,我們來探討圖 5-3 中的 MD5 演算法,他有兩組輸入:一組為 512 bits 的明文區塊(Pq),另一組為上一區塊所計算出來 128 bits 的雜湊值(CVq)(第一個區塊為 IV 值)。經由 MD5 演算法計算出 128 bits 的雜湊值(CVq+1)後,繼續傳送給下一個區塊直到結束。其實,圖 5-3 中只有一個 MD5 演算法,亦即各個區塊不斷重複使用同一個 MD5 演算法。MD5 演算法共區分為四個步驟,每個步驟須重複運算 16 次,合計共有 64 次的運算。其計算方式是將 512 bits 區分為 4 個 128 bits 的運算單位,分別存入 4 個暫存器內,在 64 次計算當中,都依照暫存器的內容來運算,並分別加入前一次的雜湊值,不僅如此,還加入 sin(x) 函數的運算,如此說來,MD5 應該夠複雜了。
圖 4-4 為 MD5 演算法的功能圖,共分為 4 個回合計算,每一回合計算 16 次。處理步驟如下:
-
步驟 1:將輸入明文(512 bits)以每 32 bits 為單位,分別存入X[k]中,其中 k =0, 1, 2, .., 15;每一回合的每一次計算分別選入不同的 X[k] 值(容後介紹)。
-
步驟 2:初始化 A、B、C 與 D 暫存器。MD5 必須產生 128 bits 的訊息摘要,而這些摘要必須利用4 個暫存器來儲存及運算,因此每個暫存器的空間是 32 bits;其初始值的設定分別如下:(16 進位表示)
A:01 23 45 67
B:89 ab cd ef
C:fe dc ba 98
D:76 54 32 10
其中數值皆以較小位元在前面的位元組(Little-endian)方式來儲存。
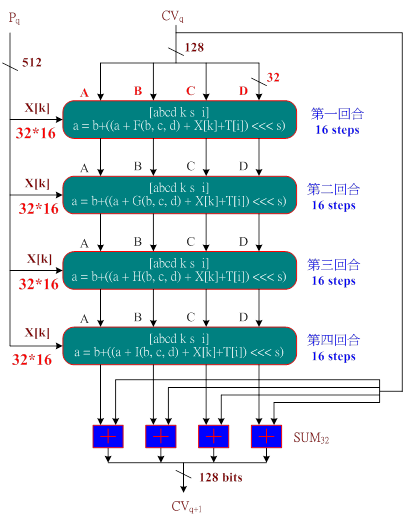
圖 4-4 MD5 演算法的功能圖
-
步驟 3:進入第一回合運算,將 A、B、C 與 D 等四個暫存器與明文輸入的 X[k],一起輸入到一個稱之為『壓縮函數』(容後介紹)內處理,此壓縮會使用到 sine 函數所建立的參數 T[i](容後介紹,圖 5-5)。每次處理的壓縮函數的輸入參數為 [abcd, k, s, i],其中 abcd 表示上一執行次數的四個暫存器、k 表示輸入明文的區段 X[k]、i 表示 sine 函數的參考值 T[i] 與 s 表示向左迴旋的次數。輸出時,bcd 三個暫存器的內容不變,但 a 暫存器修改成 a = b+((a+F(b, c, d)+X[k]+T[i]) <<<s),其中 F 函數每個回合都不同(容後介紹)。本回合需連續執行 16 次,各次的輸入參數如下:
|
[ABCD, 0, 7, 1] |
[DABC, 1, 12, 2] |
[CDAB, 2, 17, 3] |
[BCDA, 3, 22, 4] |
|
[ABCD, 4, 7, 5] |
[DABC, 5, 12, 6] |
[CDAB, 6, 17, 7] |
[BCDA, 7, 22, 8] |
|
[ABCD, 8, 7, 9] |
[DABC, 9, 12, 10] |
[CDAB, 10, 17, 11] |
[BCDA, 11, 22, 12] |
|
[ABCD, 12, 7, 13] |
[DABC, 13, 12, 14] |
[CDAB, 14, 17, 15] |
[BCDA, 15, 22, 16] |
以第二次執行為例,其輸入參數為 [DABC, 1, 12, 2](k=1, s =12, i=2),表示將上一次運算的 D、A、B、C 暫存器分別填入本次的 A、B、C 與 D 暫存器中,再計算 a = b+((a+ F(b, c, d)+ X[1] + T[12]) <<< 2),然而 B、C 與 D 暫存器的內容不變。
-
步驟 4:進入第二回合運算。同樣執行 16 次,但變更 a 的函數為 G,則 a = b+((a+G(b, c, d)+X[k]+T[i]) <<<s);每次輸入的參數如下([abcd, k, s, i]):
|
[ABCD, 1, 5, 17] |
[DABC, 6, 9, 18] |
[CDAB, 11, 14, 19] |
[BCDA, 0, 20, 20] |
|
[ABCD, 5, 5, 21] |
[DABC, 10, 9, 22] |
[CDAB, 15, 14, 23] |
[BCDA, 4, 20, 24] |
|
[ABCD, 9, 5, 25] |
[DABC, 14, 9, 26] |
[CDAB, 3, 14, 27] |
[BCDA, 8, 20, 28] |
|
[ABCD, 13, 5, 29] |
[DABC, 2, 9, 30] |
[CDAB, 7, 14, 31] |
[BCDA, 12, 20, 32] |
-
步驟 5:進入第三回合運算。同樣執行 16 次,改變 a 的函數為 H,則 a = b+ ((a+ H(b, c, d)+ X[k]+T[i]) <<<s);每次輸入的參數如下([abcd, k, s, i]):
|
[ABCD, 5, 4, 33] |
[DABC, 8, 11, 34] |
[CDAB, 11, 16, 35] |
[BCDA, 14, 23, 36] |
|
[ABCD, 1, 4, 37] |
[DABC, 4, 11, 38] |
[CDAB, 7, 16, 39] |
[BCDA, 10, 23, 40] |
|
[ABCD, 13, 4, 41] |
[DABC, 0, 11, 42] |
[CDAB, 3, 16, 43] |
[BCDA, 6, 23, 44] |
|
[ABCD, 9, 4, 45] |
[DABC, 12, 11, 46] |
[CDAB, 15, 16, 47] |
[BCDA, 2, 23, 48] |
-
步驟 6:進入第四回合運算。同樣執行 16 次,改變 a 的函數為 I,則 a = b+ ((a+ H(b, c, d)+ X[k]+T[i]) <<<s);每次輸入的參數如下([abcd, k, s, i]):
|
[ABCD, 0, 6, 49] |
[DABC, 7, 10, 50] |
[CDAB, 14, 15, 51] |
[BCDA, 5, 21, 52] |
|
[ABCD, 12, 6, 53] |
[DABC, 3, 10, 54] |
[CDAB, 10, 15, 55] |
[BCDA, 1, 21, 56] |
|
[ABCD, 8, 6, 57] |
[DABC, 15, 10, 58] |
[CDAB, 6, 15, 59] |
[BCDA, 13, 21, 60] |
|
[ABCD, 4, 6, 61] |
[DABC, 11, 10, 62] |
[CDAB, 2, 15, 63] |
[BCDA, 9, 21, 64] |
很顯然的,MD5 演算法是經過 64 次的重複計算,類似攪拌機的功能,完全將 512 bits 資料的關聯攪碎。光攪拌還是無法消除位元之間的連帶性,因此,每一次攪拌時再加入一些『鹽』(Salt),使其更加混擾,類似『醃製法』(Salt Value)的功能。至於採用何種『鹽』會比較沒有關聯性,就 MD5 而言,它使用 Sine 函數的非線性數值特性,計算方式是 T[i] = 232 × (abs(sin(i)),其中 i 表示弧度(Radians),i 由 1 到 64;亦即每一次運算取一個鹽 T[i],共64 次運算,剛好由 T[1] 取到 T[64],T[i] 的數值如圖 4-5 所示。另外,每一次運算時,會輸入 32 個位元的明文(X[k]),原區塊的明文倍分割為 16 的段落(X[0], X[1], …, X[15]),也會在這 64 次計算中重複被輸入。
|
T[1] = D76AA478 |
T[17] = F61E2562 |
T[33] = FFFA3942 |
T[49] = F4292244 |
|
T[2] = E8C7B756 |
T[18] = C040B340 |
T[34] = 8771F681 |
T[50] = 432AFF97 |
|
T[3] = 242070DB |
T[19] = 165E5A51 |
T[35] = 699D6122 |
T[51] = AB9423A7 |
|
T[4] = C1BDCEEE |
T[20] = E9B6C7AA |
T[36] = FDE5380C |
T[52] = FC93A039 |
|
T[5] = F57COFAF |
T[21] = D62F105D |
T[37] = A4BEEA44 |
T[53] = 655B59C3 |
|
T[6] = 4787C62A |
T[22] = 02441453 |
T[38] = 4BDECFA9 |
T[54] = 8F0CCC92 |
|
T[7] = A8304613 |
T[23] = D8A1E681 |
T[39] = F6BB4B60 |
T[55] = FFEEF47D |
|
T[8] = FD469501 |
T[24] = E7D3FBC8 |
T[40] = BEBFBC70 |
T[56] = 85845DD1 |
|
T[9] = 698098D8 |
T[25] = 21E1CDE6 |
T[41] = 289B7EC6 |
T[57] = 6FA87E4F |
|
T[10] = 8B44F7AF |
T[26] = C33707D6 |
T[42] = EAA127FA |
T[58] = FE2CE6E0 |
|
T[11] = FFFF5BB1 |
T[27] = F4D50D87 |
T[43] = D4EF3085 |
T[59] = A3014314 |
|
T[12] = 895CD7B1 |
T[28] = 455A14ED |
T[44] = 04881D05 |
T[60] = 4E0811A1 |
|
T[13] = 6B901122 |
T[29] = A9E3E905 |
T[45] = D9D4D039 |
T[61] = F7537E82 |
|
T[14] = FD987193 |
T[30] = FCEFA3F8 |
T[46] = E6DB99E5 |
T[62] = BD3AF235 |
|
T[15] = A679438B |
T[31] = 676F02D9 |
T[47] = 1FA27CF8 |
T[63] = 2AD7D2BB |
|
T[16] = 49B40821 |
T[32] = 8D2A4C8A |
T[48] = C4AC5665 |
T[64] = EB86D391 |
圖 4-5 sin(x) 函數所建立的『鹽』
4-3-3 MD5 壓縮函數
每一回合的運算器稱之為『壓縮函數』(Compression Function),是 MD5 演算法的核心。它的功能是將 512 個位元的區塊,攪拌及壓縮成 128 個位元,其運算程序如圖 4-6 所示,各暫存器的運算式為:
a = b + ((a + g(b, c, d) + X[k] + T[i]) <<< s)
b = b, c = c, d = d
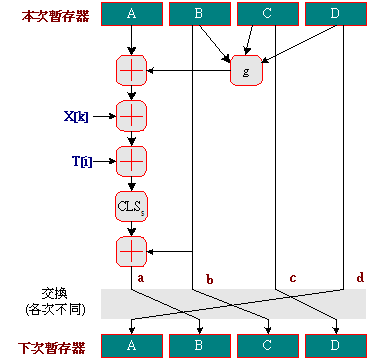
圖 4-6 MD5 壓縮函數的功能圖
其中:
-
a, b, c, d:為四個 32 位元的暫存器。
-
g:每一回合有不同的基本函數,分別是 F、G、H 與 I。
-
<<< s:表示向左迴旋 s 個位元。
-
X[k]:表示區塊明文中的第 k 個 32 位元字元。
-
T[i]:表示圖 5-5 中的 Sine 函數值。
-
+ :取 32 位元的同餘加法(mod 232)。
上述的意思是,每次(每回合有 16 次)只針對暫存器 a 的內容做運算,而 b、c 與 d 的內容不變;計算後的 a、b、c、d 暫存器分別填入下次的 B、C、D、A(各次皆不相同),做為下一次計算的暫存器內容。且每一回合(計有四個回合)的基本函數 g 亦不相同。MD5 利用 4 個邏輯運算子,來實現基本函數,分別是 AND(符號: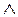 )、OR( )、OR(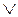 )、NOT( )、NOT(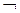 )與 XOR(⊕),各個回合的基本函數歸類如下: )與 XOR(⊕),各個回合的基本函數歸類如下:
函數 F 是一個條件函數:If b then c else d;同樣的,G 也是條件函數:If d then b else c;函數 H 是互斥或產生一個同位位元(Parity bit);函數 I 是:If c then (b or not d) else (not b or d)。
對 MD5 而言,每四個回合都有一個基本函數(F、G、H 與 I),並且每一回合都計算 16 次;基本上,以 128 bits 的雜湊值而言,它是非常安全的。但對生日攻擊法而言,只要搜尋 264 的偽造訊息,仍然可以找出相同的雜湊值,就目前電腦速度來講,其安全性已漸堪慮。
|

翻轉工作室:粘添壽
資訊與網路安全技術
翻轉電子書系列:
|