![]() 翻轉工作室:粘添壽
翻轉工作室:粘添壽
第三章 現代公開鑰匙系統
![]() 『現代密碼學』,係利用數論的同餘運算,所推演出來的密碼演算法,由於同餘算術可以找出反函數,因而演變出一場兩把鑰匙的遊戲;無論如何,在未發現破解函數之前,它還是安全的。
『現代密碼學』,係利用數論的同餘運算,所推演出來的密碼演算法,由於同餘算術可以找出反函數,因而演變出一場兩把鑰匙的遊戲;無論如何,在未發現破解函數之前,它還是安全的。
西元 1970 可說是密碼學百花齊放的年代,密碼學領域裡出現三組偉大的開啟者。首先是 Feistel 於 1973 提出的乘積與重複編碼技巧,不但開啟區塊加密編碼的大門,時至今日大部分秘密鑰匙系統(對稱加密系統)還是沿用此架構。接著 Diffie 與 Hellman 於 1976 年提出鑰匙交換的基本架構,仍是目前各種鑰匙交換協定主要的基礎。此外,他們又提出一個單向暗門函數密碼學的基本架構和『數位簽章』(Digital Signature)的概念,只是當時他們並不知道單向暗門是否真的存在。到了 1978 年,才由美國麻省理工學院(MIT)三位先進(Rivest、Shamir 與 Adleman)率先提出一個藉由分解因數之指數函數作為單向暗門的函數 [117],從此開啟了『公開鑰匙密碼系統』(Public Key Cryptosystem,或簡稱公開鑰匙系統)的序幕。
『公開鑰匙密碼學』與秘密鑰匙是迥然不同的演算法。秘密鑰匙密碼學是利用取代與重排的技巧來達成加密編碼的功能,故稱之為『傳統密碼學』(Conventional Cryptography);然而公鑰密碼學完全不再採用取代與重排的技巧,而是依照『數據理論』(Number Theory) 原理所發展出來,因此又稱為『現代密碼學』(Modern Cryptography)。
3-1-1 公鑰系統之架構
『公開鑰匙密碼系統』是加密與解密時所使用的鑰匙不同,又稱為『非對稱式密碼系統』(Asymmetric Cryptosystem)。此概念最早是由 1976 年由史丹佛(Standford)大學兩位先進 Diffie 和 Hellman 率先提出,期望除了加密和解密鑰匙不同之外,並要求解密鑰匙也不能由加密鑰匙求得。在他們的方案中,假設加密編碼 E、解密編碼 D 與明文 P,需滿足下列三點要求:
D (E (P)) = P。
由 E 很困難推演出D。
E 不會被選定明文攻擊法破解。
第一個條件是,明文經過加密編碼法 E 處理後產生的密文,可以利用解密編碼法 D將他回復原來的明文 P。第二個條件是,由加密編碼法 E 中很難推演出解密編碼法 D。至於第三個條件即是抗拒明文攻擊能力(如同 2-3 節介紹)。他們提出這三個問題是希望解決數位簽章的『不可否認性』功能。因此,在提案中期望某一個編碼演算法必須是公開的,如此一來,防護選擇明文攻擊的能力就必須強一點。比如說,攻擊者選擇某些明文並利用 E 演算法(假設是公開的)加密,並利用所得到密文來破解 D 演算法(假設是隱密的)。當時 Diffie-Hellman 僅提出這個概念,並無提出解決方案,直到 1978 年才由 Rivest、Shamir 與 Adleman 等三人共同提出公鑰編碼系統架構出來。圖 3-1 為公開鑰匙系統的基本架構,其基本要素如下:
每一位參與者(或系統)都擁有一對鑰匙,用來對訊息加密與解密。其中一把若作為加密,則另一把則為解密使用。即是,明文如用公開鑰匙加密得到密文,則須利用私有鑰匙將密文解密得到原來明文,反之亦然。
參與者(或系統)會將其中一把鑰匙公佈在一個公開的註冊或檔案,該鑰匙便稱為『公開鑰匙』(Public Key, KU);另一把鑰匙必須隱密的收藏著,不可洩漏給他人知道,因此稱之為『私有鑰匙』(Private Key, KR)。
通訊雙方皆須持有鑰匙配對中一把鑰匙;如果一方持有公開鑰匙,另一方必須擁有私有鑰匙;反之亦然。
加密與解密程序,有各自的演算法(E 或 D)與鑰匙(KU或 KR)。
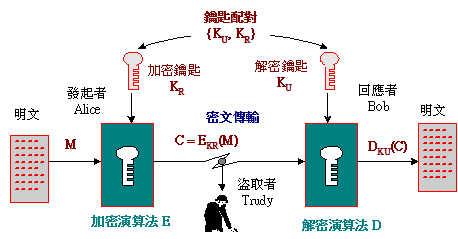
圖 3-1 公開鑰匙系統架構
以上是假設參與運作者都擁有鑰匙配對,但某些應用只要某一方持有鑰匙配對即可。我們用數學式子來表示圖 4-1 的運作程序,假設明文為 M、鑰匙配對為 {KR, KU}、C 為密文。其加密與解密程序為:
加密程序:![]() ,利用 KR加密。
,利用 KR加密。
解密程序:![]() ,利用 KU解密。
,利用 KU解密。
至於上述式子中會用到哪一方的鑰匙配對,這屬於公開鑰匙系統所扮演的角色問題,我們下一節再介紹。
3-1-2 公鑰系統之演算法
公開鑰匙演算法之所以異於秘密鑰匙密碼學,它不再採用『換位與取代』方式,完全利用數學推導而成,其中又以『數論』(Number Theory)的同餘算術為主軸,目前較常見的演算法有:
『RSA 演算法』(RSA Algorithm):由 RSA 資料安全公司(RSA Data Security Inc.)所推行,使用於資料加密與數位簽章(4-3節介紹)。
『橢圓曲線密碼學』(Elliptic Curve Cryptography, ECC):本書未介紹,有興趣讀者可參考密碼學相關書籍 [79, 89, 98]。
『Diffie-Hellman 演算法』(Diffie-Hellman Algorithm):主要應用於鑰匙交換,已被崁入許多鑰匙交換協定之中(4-4節介紹)。
『數位簽章標準』(Digital Signature Standard, DSS):主要使用於數位簽章,第七章再介紹。
『ELGamal 演算法』(ELGamal Algorithm):主要應用於數位簽章,本書未介紹。
當然,還有許多公鑰演算法被提出來,本書侷限於篇幅並無法一一介紹,讀者對這方面有興趣的話,請參閱其它密碼學書籍。
3-2 公開鑰匙的數學基礎
『數論』(Number Theory)是公開鑰匙密碼學的理論基礎,本節就相關部份做簡單介紹,讀者若有興趣可參考。
『質數』(Prime)是密碼系統主要計算數值,因為密碼系統大多採用『模數』(Modulo)算術推論出來的。質數在『模數』運算裡出現的重複性最低,計算結果最能接近『唯一性』。
『質數』(Prime):一個只能被 1 或自己整除的數值,稱之為質數。質數是除了 1 和自己之外,除以小於本身的任何數都會有餘數,下列是1 到 100 之間的質數:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 |
一般在加密演算法裡常出現尋找質數的問題,並且為了不讓他人猜測出所找的數為何,都會選擇一個較大的數值範圍。就實際觀點而言,欲尋找一個很大的質數並非易事,一般可能利用亂數函數隨機取一個數,再測試這個數是否為質數(有關測試質數演算法可參考 [1, 7, 136])。接下來,簡單介紹質數的特性。
對任意 a >1的數,可以被分解成:
![]()
其中,p1, p2, …, pi都是質數,且 p1 < p2 < p3 < …< pi,每個 αpi > 0。也就是說,任何一個數都可分解成質因數的乘積。譬如:
3600 = 24× 32× 52
其中: p1 = 2、α2 =4(因 p1 = 2,則αp1 =α2);
p2 = 3、α3 =2(因 p2 = 3,則αp2 =α3);
p3 = 5、α5 =2(因 p3 = 5,則αp3 =α5)。
如果想要計算兩個數的乘積,可由相關質因數的指數(αpi)來計算(指數的和),譬如,216 = 12 × 18,可由下列計算得到:
12 = 22× 31,則α2 =2、α3 =1。
18 = 21× 32,則α2 =1、α3 =2。
216 = 23× 33,因為α2 =2 + 1= 3、α3 =1 + 2 =3。
3-2-2 互質數
若 gcd(a, b) 表示 a 和 b 的最大公因數,則 gcd(a, b) = 1表示 a 與 b 互質;也就是說,a 與 b 之間除了 1 之外,沒有其他公因數。現在我們來觀察如何計算出兩數之間的最大公因數。首先將任意兩數分解出其對應的質因數冪次方的乘積,接著選取較低冪次方的因子,將這些因子相乘便是兩數的最大公因數。譬如,欲找出 18 與 300 兩數的最大公因數 gcd(18, 300),可由下列計算式得到:
300 = 22× 31× 52;
18 = 21× 32× 50,則:
gcd(300, 18) = 21× 31× 50 = 6
上述尋找最大公因數的例子,看似簡單,其實對一個很大的數做質因數分解並非易事,目前雖有一些相關演算法,但其複雜度仍然偏高,這方面尚有研究空間。話說回來,找出兩個質數且具有互質條件,可說是公開密碼演算法精髓所在。至於如何尋找兩個互質的質數?這方面就留給讀者慢慢去探討。
3-3 公開鑰匙的同餘算術
『同餘算術』(Modular Arithmetic)是表示某一進位的運算,譬如有二進位運算、八進位運算、十六進位運算、或 n 進位運算(n 為任何數)。較常使用的同餘算術有加法、乘法和指數運算,其中同餘指數可說是同餘乘法一個特例(譬如 X3是 X × X × X),但它是公鑰系統的主要運算工具。在公鑰系統中有一個重要觀念,即是『反函數』(Inverse Function),表示某數經由演算之後,是否可以由另一個數值找出原來的值。譬如 X 經由計算後得到 Y,是否可以找到另一個數 Z,再由 Y 與 Z 計算出原來的值 X;如果可以的話,Z 便是 X 的反函數。我們試著利用各種同餘算術的推導,來找出是否具有反函數的功能(反向加法或反向乘法),再利用反函數來推論出公鑰系統的公開與私有鑰匙。反向函數又稱為『反向暗門』(Inverse Backdoor),理想狀態反向暗門必須是唯一的;因而,稱之為『單向暗門』。
所謂『模數』(Modulo)是一種除法取餘數的運算,譬如某數modulo 16、modulo 10、modulo 8分別表示某數除以16、10、8的餘數,為了簡化,一般以mod表示。『模數』即是表示在某領域範圍內做運算,參與計算的運算元,以及計算後的結果都不會超過該領域範圍。譬如,modulo 8 運算,則運算元與結果都不會超過 8(0 ~ 7)範圍。如果運算結果超過 8,則取 8 的餘數。如此就非常接近 8 進位計算,但模數沒有進位,直接將進位部份捨棄。習慣上,我們常使用 10、2、8、16 進位的運算,但在密碼學上可能採用任何數(n)進位的運算,常以 modulo n 或 mod n 來表示。
令一個正整數 n 與整數 a,並 a 除以 n 得到商為 q,與餘數 b,之間的關係如下:
a = qn + b 0 ≦ b < n;q =「a/n」
其中,q =「a/n」 表示 a/n 整除的數(0 或其它大於 1 的整數);可能得到的餘數 b = {0, 1, 2, …, n-1},稱之為『完全餘數系』(Complete of Residues)。上式成立的話,可定義模數運算如下:
b ≡ a mod n
其中『≡』表示『相當於』的意思,而並非『相等』(Equal,” = “);也就是說,b 的值是相當於 a 取模數 n(a mod n)的計算,但並非僅有 a 才可能得到 b,而可能存在其它數值。譬如,a mod 10 = 6,其中 a 可能出現的情況有:6、16、26、、、等等;但這些數存在有一個特性 a = qn + 6,q 為 0 或大於 1 的整數。瞭解模數運算(mod)之後,將其具有的特性歸類如下[1, 86, 121]:
反向性:a ≡ a mod n。
(驗證: 5 ≡ 5 mod 10)
對稱性:若 a ≡ b mod n,則 b ≡ a mod n。
(驗證:5 ≡ 15 mod 10 則15 ≡ 5 mod 10 ≡ 5 = a )
遞移性:若 a ≡ b mod n 且b ≡ c mod n,則 a ≡ c mod n。
(驗證:5 ≡ 15 mod 10 且15 ≡ 25 mod 10,則 5 ≡ 25 mod 10≡ 5 = a)
若 (a mod n) = (b mod n),可推論出 a ≡ b mod n。
(驗證:(15 mod 10) = (25 mod 10),則 15 ≡ 25 mod 10≡ 5 = a)
接下來,我們利用模數特性,來推論同餘算數。
『同餘加法』(Modular Addition)表示在某個領域(或稱模組,n)內執行加法運算。基本上,參與計算數值的大小應該不會超過該領域,計算後的結果也不會超過該領域(模組 n)。假設 a = 8、b = 7、n=13,則運算結果如下:
(a + b ) mod n = (8 + 7) mod 13 = 2
上述表示在領域 13 的同餘加法運算,基本上,運算元(a 與 b)與計算後結果都不會超過 13(0 ~ 12),如果超過 13 的話,則取 13 的餘數。但許多情況下,參與計算數值的大小可能超過領域(模組 n),則取模組餘數後再計算的結果,與相加後再取模組餘數的結果相同,亦即:
[(a mod n) + (b mod n)] mod n = (a + b) mod n 式子(4.1)
吾人以 a = 16、b=24、n=13,驗證上述式子(1) 是否成立:
式子(4.1) 左邊 = ((16 mod 13) + (24 mod 13)) mod 13
= (3 + 11) mod 13
= 1
式子(4.2) 右邊 = (16 + 24) mod 13
= 40 mod 13
= 1
則式子(1) 左邊運算結果與右邊相同,該式子成立。此特性對我們推演 RSA 演算法很有幫助。
我們將 modulo 10 的加法,由 0 到 9 之間數字相加的結果顯示於圖 4-3。
+ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
2 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
3 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
4 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
5 |
5 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
6 |
6 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
7 |
7 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
8 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
9 |
9 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
圖 4-3 Modulo 10 的加法
接著來探討同餘加法是否具有反向函數的功能。假設以 mod 10 為例,而明文、公開鑰匙、私有鑰匙、以及密文都介於 0 ~ 9 之間。由圖 4-3 可以明顯觀察出 mod 10 具有非對稱加/解密功能,其中公開鑰匙 KU與私有鑰匙 KR之間的關係是 KU + KR = 10,且加密與解密演算法都是同餘加法運算(mod 10),下列是1 ~ 9 之間加密與解密鑰匙的配對關係:
公開鑰匙 (KU): |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
私有鑰匙 (KR): |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
譬如,KU = 4、KR = 6、明文 P=5,則利用公開鑰匙加密得密文 C = KU +5 = 4+5 ≡9 mod 10,再利用私有鑰匙解密,還原明文為 P = KR + 9 = 6+9≡5 mod 10。
由此可見,KU與 KR之間的關係是互為反向函數,亦即若以 KU加密的密文,便可以利用 KR解密回來,反之亦然。KU與 KR的關係如下(以 mod 10 為例):
KU + KR = 10
亦即:
KU + KR≡0 mod 10
因此,我們可以做一個簡單的結論,同餘加法具有反向函數的能力,又稱之為『加法反向』(Addition Reverse)。假設同餘模數為 n,任何數值 y,與其反向元素為y-1,如果滿足『反向函數』,則兩數之間的關係為:
y + y-1≡ 0 mod n 或 y + y-1 mod n≡ 0
也就是說,在任何模數(n)運算中,只要找出兩個數的和,可以整除 n 的話,則該兩數互為加法反向函數。
『同餘乘法』(Modular Multiplication)的概念如同加法一樣,在某一領域內(模組 n)執行乘法運算。基本上,運算元(a、b)與運算結果都不會超過其領域,假設 a = 8、b = 7、n=13,則運算程序如下:
(a × b) mod n = (8 × 7) mod 13 = 56 mod 13 = 4
在許多情況下,運算元還是可能超領域。同餘乘法還是滿足,運算元取模組餘數後相乘,與相乘後再取模組餘數,兩者結果相同,亦即:
((a mod n) × (b mod n)) mod n = (a × b) mod n (式子4.2)
吾人以 a = 16、b=24、n=13,驗證上述式子(1) 是否成立:
式子(4.2) 左邊 = ((16 mod 13) * (24 mod 13)) mod 13
= (3 * 11) mod 13
= 33 mod 13
= 7
式子(4.2) 右邊 = (16 * 24) mod 13
= 384 mod 13
= 7
上述左邊運算結果與右邊相同,則式子(4.2) 成立。吾人可觀察出一個重要的特性,式子(4.2) 左邊所計算處理的數值較小,相對的所需的運算量也較少。RSA 演算法大多利用此特性來減低計算量的(容後說明)。
我們也是希望由同餘乘法的特性中,尋找出有關公鑰系統的機能。首先,將 0 ~ 9 之間互相乘積的 mod 10 列於圖 4-4,再來觀察同餘乘法的特性。
× |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
2 |
0 |
2 |
4 |
6 |
8 |
0 |
2 |
4 |
6 |
8 |
3 |
0 |
3 |
6 |
9 |
2 |
5 |
8 |
1 |
4 |
7 |
4 |
0 |
4 |
8 |
2 |
6 |
0 |
4 |
8 |
2 |
6 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
0 |
5 |
6 |
0 |
6 |
2 |
8 |
4 |
0 |
6 |
2 |
8 |
4 |
7 |
0 |
7 |
4 |
1 |
8 |
5 |
2 |
9 |
6 |
3 |
8 |
0 |
8 |
6 |
4 |
2 |
0 |
8 |
6 |
4 |
2 |
9 |
0 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
圖 3-2 Modulo 10 的乘法
圖 3-2 中,只有 {1, 3, 7, 9} 可做加/解密演算法的鑰匙(原因後述),至於公開與私有鑰匙之間的關係如下:
公開鑰匙 (KU): |
1 |
3 |
7 |
9 |
私有鑰匙 (KR): |
1 |
7 |
3 |
9 |
譬如,KU = 3、KR = 7、明文 P=4,則利用加密程序可計算密文:
C = KU× P = 3 × 4 ≡ 2 mod 10;則密文為 2。
解密程序可還原明文:
P = KR× C = 7 × 2 ≡ 4 mod 10;則明文為 4。
公開鑰匙又稱為私有鑰匙的同餘乘法反元素,因此,同餘乘法也具有公開鑰匙演算法的特性。兩者之間關係為 KU× KR≡1 mod 10。
利用同餘乘法所推演出來的反向函數,稱之為『乘法反向』(Multiplicative Reverse)。設同餘模數為 n,任何數值 y,與其反向元素為y-1,如果滿足『乘法反向』,則兩數之間的關係為:
y × y-1≡ 1 mod n 0 < y < n;0 < y-1 < n (式子 4.3)
也就是說,在任何模數(n)運算中,只要找出兩個數的乘積,除以 n 得到餘數是 1 的話,則該兩數互為加法反向函數。 式子 4.3 必須當 y (或 y-1) 與 n 互質才會成立,有關證明方面請參考[1, 86, 92],以下舉兩個例子分別說明之。
例1:若 a = 3, n = 10。因為 3 與 10 互質,所以存在一個 b (0 < b < 10)使得
a × b ≡ 1 mod n ( 3 × 7 ≡ 1 mod 10, b = 7)
例2:若 a = 5, n = 10。因為 5 與 10 不互質,所以找不到一個 b (0 < b < 10)滿足式子(4.1)。
因此利用同餘乘法依然存在公開鑰匙系統的鑰匙配對,只要找到一個 a ( < n ) 與 n 互質,必然存在一個 b ( < n ) 符合式子(4.1),當然若 n 是質數,則每一個a ( < n ) 皆與 n 互質。
『同餘指數』(Modular Exponentiation)運算即是在某領域內(模組 n)執行指數運算。基本上,參與運算元與結果的大小都不會超過該領域,譬如 a =4、b=6、n=13,則運算程序如下:
ab mod n = 46 mod 13 = 4096 mod 13 = 1
吾人可以發現,指數運算不需較大的數值參與運算,就可能產生非常大的運算量,沒經過特殊方法運算,幾乎很難完成指數運算(RSA 主要運算方法)。與同餘乘法相同,數值取模組餘數後再執行運算的結果,與執行指數運算後,再取模組餘數的結果相同,亦即:
(a mod n)b mod n = ab mod n (式子 4.4)
吾人以 a = 16、b=4、n=13,驗證上述式子 (4.4) 是否成立:
式子 (4.4) 左邊 = (16 mod 13)4 mod 13
= 34 mod 13
= 81 mod 13
= 3
式子 (4.4) 右邊 = 164 mod 13
= 15536 mod 13
= 3
依照上述驗證,式子 (4.4) 左邊與右邊運算結果相同,式子成立。吾人也可以發現右邊的計算量非常大,如果能轉換成左邊計算方法,將可以減低許多運算量。吾人大都利用此特性來實現 RSA 演算法。
接著,必須推演同餘指數是否具有反向暗門特性,藉此觀察是否利用它來實現非對稱密碼系統。圖 4-5 為 0 ~ 9 之間 mod 10 的運算結果,表內數字為 xy的結果,其中 x 為列的數字;y 是行的數字。
xy |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
4 |
8 |
6 |
2 |
4 |
8 |
6 |
2 |
3 |
1 |
3 |
9 |
7 |
1 |
3 |
9 |
7 |
1 |
3 |
4 |
1 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
6 |
4 |
5 |
1 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
6 |
1 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
6 |
7 |
1 |
7 |
9 |
3 |
1 |
7 |
9 |
3 |
1 |
7 |
8 |
1 |
8 |
4 |
2 |
6 |
8 |
4 |
2 |
6 |
8 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
1 |
9 |
圖 3-3 modulo 10 的指數運算
其實指數運算表示自我函數相乘的次數,如 X3表示 X 自我相乘 3 次。同餘指數是同餘乘法運算的延伸,它的反向函數也與同餘乘法相同,如下:(公式 4.3)
y × y-1≡ 1 mod n
由圖 3-3 可以找出合乎反向暗門條件的鑰匙 KU(y)與 KR(y-1)如下:(n = 10)
公開鑰匙 (KU): |
1 |
3 |
7 |
9 |
私有鑰匙 (KR): |
1 |
7 |
3 |
9 |
譬如,明文 P = 8、公開鑰匙 KU = 3、私有鑰匙 KR = 7,則加密程序為:
加密:密文 C = ![]() = 83≡ 2 mod 10;則密文為 2。
= 83≡ 2 mod 10;則密文為 2。
解密程序為:
解密:明文 P = ![]() = 27≡ 8 mod 10;則明文為 8。
= 27≡ 8 mod 10;則明文為 8。
同樣的,將利用私有鑰匙加密,也可利用公開鑰匙還原。吾人可證明出同餘指數運算具有反向暗門(乘法反向),兩支鑰匙之間的關連為 KU× KR≡1 mod 10(與同餘乘法相同)。
Euler’s Totient 函數 ψ(n) 是公開鑰匙演算法中重要的參數,其意思是小於 n 但與 n 互質之正整數的數目,譬如ψ(10) = 4,因為小於 10 且與 10 互質的正整數共有 4 個 (1, 3, 7, 9)。圖 4-6是ψ(n), 0 < n < 31, 的函數值。
n |
ψ(n) |
n |
ψ(n) |
n |
ψ(n) |
1 |
1 |
11 |
10 |
21 |
12 |
2 |
1 |
12 |
4 |
22 |
10 |
3 |
2 |
13 |
12 |
23 |
22 |
4 |
2 |
14 |
6 |
24 |
8 |
5 |
4 |
15 |
8 |
25 |
20 |
6 |
2 |
16 |
8 |
26 |
12 |
7 |
6 |
17 |
16 |
27 |
18 |
8 |
4 |
18 |
6 |
28 |
12 |
9 |
6 |
19 |
18 |
29 |
28 |
10 |
4 |
20 |
8 |
30 |
8 |
圖 3-4 Euler’s Totient 函數
由圖 3-4 可以觀察出來,如果 p 為質數的話(圖中有陰影的欄位),則:
ψ(p) = p-1
譬如,p=3,則ψ(3) = 3-1=2;p=19,則 ψ(19) = 18;依此類推。現在假設有兩個質數 p 與 q,且 n = pq,則:(證明請參考 [1, 92])
ψ(n) =ψ(pq) =ψ(p) × ψ(q) = (p-1) × (q-1) (式子 4.7)
驗證,如果 p=3、q=7,所以n = 3 × 7 = 21,則:
ψ(21) =ψ(3) × ψ(7) = (3-1) × (7-1) = 2 × 6 = 12(如同圖 4-6 所示)
我們來回顧一下ψ(n) 的特性,它代表著與 n 成為『互質』的數目。在同餘運算中,質數經由某一數運算之後,最有可能產生餘數,這也是推論公鑰演算法的最基本要素。因此,ψ(n) 的數值愈大,則可能選用的質數就愈多,以圖 4-5 為例(同餘指數運算),ψ(10) = 4,則可選用與 10 互質的數只有四個(1, 3, 5, 7),並且運算結果每 4 列便再重複。
3-4 RSA 演算法
RSA 的名稱是由 Rivest、Shamir 與 Adleman 三人的名字共同組合而成。雖然 Diffie 與 Hellman 提出只要能找出單向暗門的數學函數,便能解決公鑰密碼學的問題。但真正提出解決方案的是由 Rivest、Shamir 與 Adleman 等三人,也因此定名為『RSA 演算法』(RSA Algorithm)。
依據 RSA 演算法特點,大多運用於密鑰交換與數位簽章兩大方面。其實 RSA 演算法也可以用來加密與解密功能,達成訊息隱密性傳輸的功能。但它為了提供安全性,鑰匙長度都較長,執行加密與解密時,需耗費較長的時間,因此對於大量資料傳輸並不適合。
利用 RSA 鑰匙加密的特點是,『明文的長度不可以超過鑰匙長度』(根據不同補齊方式,能夠加密的長度也不一樣),訊息經由加密編碼後的密文與鑰匙長度相同。如果針對大量資料加密的話,則需將明文依照鑰匙長度(如 1024 或 2048 bits)分割成若干個區塊,分別加密後再組合成密文序列。解密處理也是相同,分段解密後再組合回原明文格式。
RSA 演算法配合雜湊演算法執行數位簽章就容易多了,原始文件經由雜湊演算法(SHA1、MD5)編碼後,產生 160 位元或 128 位元,再經由 RSA 私有鑰匙(簽署)或公開鑰匙(驗證)加密,所耗費的時間就較短。
RSA 演算法是利用同餘指數,推演出公開與私有鑰匙配對,並能完全合乎單向暗門的需求。RSA 演算法同樣使用區塊加密法,且鑰匙與區塊明文的長度必須相同(一般情況下都使用 512 個位元的長度)。明文區塊被加密成相同長度的密文區塊,每一區塊的數值小於某個整數 n,表示區塊的大小必須小於或等於log2(n)位元,若區塊大小為 k 個位元,則 2k < n < 2k+1。對於明文 M 與密文區塊 C 來說,其加密與解密程序為:
C ≡ Me mod n
M ≡ Cd mod n ≡(Me)d mod n ≡ Med mod n
其中 n 為加密者與解密者雙方都知道的數值,但加密者必須知道數值 e,而只有解密者知道另一個數值 d,我們以 KU = {e, n}為公開鑰匙,以 KR = {d, n} 為私有鑰匙;兩把鑰匙可以相互加密或解密。
為了滿足上述 RSA 演算法的特性,必須合乎下列條件:
必須找出 e、d 與 n 的值,使得對所有 M < n 來說,都能滿足 Med≡ M mod n。
對任何 M < n 而言,計算 Me與 Cd都必須非常容易。
如果給定 e 與 n,要計算出 d 是非常困難的。
第一個問題是主要的關鍵,Med≡ M mod n 的意思是 Med除以 n 所得到的餘數是 M;而 Med是 M 經由加密後 Me再解密運算 Cd後所得到的明文,依照 Euler 定理(式子 4.9,條件 m 與 n 互質):
mψ(n)+1 ≡ m mod n
我們給定兩個質數 p 與 q,以及兩個整數 n (=p × q) 與 m,其中 0 < m < n,則下列關係式必然成立:(引用式子 4.7)
mψ(n)+1 = m(p-1)(q-1)+1≡ m mod n
接著,討論質數 p 與 q 的關係。依照 Euler 定理,m 必須與 n 成為互質(gcd(m, n) = 1),則上述的式子成立;又 n = pq,是否表示 p 與 m、或 q 與 m 也成為互質?但 a 與 m 成為互質的話,p 與 q 兩者之間必定至少有一個數,必須與 m 成為互質。因此,假設如下:
m = pc,其中 c 為任何整數。
gcd(m, p)≠1 與 gcd(m, q) =1。
由條件 (2) 是假設 m 與 p 之間不構成互質,因此存在著 m = pc 的關係;另外假設 m 與 q 之間構成互質關係。如果 gcd(m, q) = 1。依照 Euler 定理,下列式子一定成立:(式子 4.8)
mψ(q) ≡ 1 mod q
接著,再利用同餘運算的規則:(備註:1k = 1)
[mψ(q)]ψ(q) ≡ 1 mod q
mψ(p)×ψ(q) ≡ 1 mod q
m(p-1)×(q-1) ≡ 1 mod q;又ψ(n) = (p-1)×(q-1) 則:
mψ(n) ≡ 1 mod q
上述式子表示存在一個 k 的關係,而 k 為任何數值的整數:
mψ(n) = 1 + kq
等號雙邊同乘以 m,並且 m = pc(假設條件 (1))與 n = pq,則:
mψ(n)+1 = m + ckpq = m + ckn
所以
mψ(n)+1 ≡ m mod n
由此可見,只要 gcd(m, q) =1 成立的話,則上式成立;因此,不管m與n是否互質,下列式子必然成立:
mkψ(n)+1 = mk(p-1)(q-1)+1≡ m mod n (式子 4.10)
驗證如下: mψ(n) ≡ 1 mod n [mψ(n)]k≡ 1 mod n mkψ(n) ≡ 1 mod n mkψ(n)+1 = mk(p-1)(q-1)+1≡ m mod n |
我們可以回到 Med≡ M mod n 的推演,只要:
ed = kψ(n) +1
則下列式子就成立:
Med≡ M mod n
所以:
ed ≡ 1 mod ψ(n)
d ≡ e-1 mod ψ(n)
由此可以大略了解 e、d 與 n 之間的關係。意即在取ψ(n) 的同餘運算之下,e 與 d 互為乘法反函數。又 ed ≡ 1 mod ψ(n) 表示 e 與 d 中必須有一個數與ψ(n) 互質,才可以成立;意即需要:
gcd(ψ(n), e) =1 或
gcd(ψ(n), d) =1;兩條件之一成立。
一般將選用互質的數(如 e)當作公開鑰匙,而不一定成為互質的數(如 d)做為私有鑰匙。
經過上述的推論之後,我們可以將 RSA 演算法的相關參數歸類如下:
p 與 q 兩質數:自行選擇的私有值。
n=pq:計算而得的公開值,並且求出 ψ(n) = (p-1)(q-1) 的值。
選擇 e,需滿足 gcd(ψ(n), e)=1;1 < e <ψ(n):自選公開值。
d ≡ e-1 mod ψ(n):計算而得的私有值。
公開鑰匙由 {e, n} 所組成,而私有鑰匙則由 {d, n} 組成,e 與 d 之間的關係是:
ed ≡ 1 mod ψ(n)
則 ed = kψ(n) +1,又依照 Euler 定理(式子 4.6):
Mkψ(n)+1 ≡ Mk(p-1)(q-1)+1≡ M mod n
因此,可以證明出下式:
Med = Mkψ(n)+1
Med≡ M mod n
得到上式之後,可將 RSA 演算法的運作程序歸類如下(同餘指數運算):
明文區塊:M
公開鑰匙:{e, n}
私有鑰匙:{d, n}
加密編碼:C ≡ Me mod n
解密編碼:M ≡ Cd mod n ≡ (Me)d mod n ≡ Med mod n ≡ M mod n
接下來,我們用一個範例說明公開鑰匙與私有鑰匙的產生方式,如下:
選定兩個質數,p = 7、q = 17。
計算 n = pq = 7 × 17 = 119。
計算ψ(n) = (p-1) × (q-1) = 6 × 16 = 96。
選定 e,但必須滿足 gcd(e, ψ(n)) =1,假設選擇 e =5,因與 96 互質。
(備註:由 3, 5, 7, … 質數開始測試是否滿足)
(備註:de/96 = 商 .. 餘數 1,則 d×5 = (96×y) +1,由 y=1, 2, 3, .. 開始測試)
經過上述推演得到:
公開鑰匙:KU = {e, n} = {5, 119}
私有鑰匙:KR = {d, n} = {77, 119}
我們用一個明文 M=19,來測試加密與解密的運作程序,如下:
加密編碼:C ≡ Me mod n ≡ 195 mod 119 ≡ 66 mod 119,則密文為 66。
演算過程如下: 192 = 361 ≡ 4 mod 119 194≡ 4 × 4 = 16 ≡ 16 mod 119 195 = 194× 191≡16 × 19 = 304 ≡ 66 mod 119 |
解密編碼:M ≡ Cd mod n ≡ 6677 mod 119 ≡ 19 mod 119,則明文為 19。
演算過程如下: 662 = 72 mod 119 664 = 72 × 72 = 5184 = 67 mod 119 668 = 67 × 67 = 4489 = 86 mod 119 6616 = 86 × 86 = 7396 = 18 mod 119 6632 = 18 × 18 = 324 = 86 mod 119 6664 = 86 × 86 = 7396 = 18 mod 119 6677 = 6664× 668× 664× 66 = 6845256 = 19 mod 119 |
攻擊 RSA 演算法有兩種主要的方法:
暴力攻擊法:嘗試所有可能的鑰匙。任何一種密碼演算法都可以被暴力攻擊破解,唯一克服的方法是增加鑰匙的長度。RSA 也是以增加鑰匙長度來克服暴力攻擊。
數學攻擊法:既然 RSA 演算法是利用數學理論推導出來,所以也一定可以利用數學方法來破解;雖然目前無法百分之一百的成功,但相信新的數學方法被推演出來時,可能致使 RSA 變得不堪一擊。目前大多採用因數分解法來攻擊 [122]。
如果要增加鑰匙長度,e 與 d 的位元數當然是愈大愈好,則相對應的 p、q 與 n 的數值也必須選擇很大的值。如此一來,所需的計算量變得非常的複雜,系統執行速度也會變慢。至於因數分解法,可有下列三種攻擊法:
將 n 分解成兩個質因數 p 與 q,如此便可以計算出ψ(n) = (p-1)(q-1),因為一般 e 都採用某一固定值(如 e =3),接著就可以計算出 d ≡ e-1 mod ψ(n)。
由 n 計算出 ψ(n),而不必先算出 p 和 q,也可以尋找出 d ≡ e-1 mod ψ(n)。
直接找出 d,而不必先計算出 ψ(n)。
基本上,還是利用分解因數,由 n 來找出 p 與 q 的攻擊方法比較可行。由上一節的分析,大略可以了解 p 與 q 的選擇是介於 1075到 10100之間,且 n = pq,符合此條件的 p 與 q 也許很多,所以目前大多採用『二次篩選法』(Quadratic Sieve)與『一般數域篩選法』(Generalized Number Field Sieve)等兩種因數分解方法。我們無法說 RSA 演算法是絕對安全,但以目前來講,它還是安全的。
3-6 Diffie-Hellman 鑰匙交換法
目前許多廠商皆採用 Diffie-Hellman『鑰匙交換』(Key Exchange)技術,製作公開鑰匙系統,但此演算法並不直接使用於加密或數位簽章,而僅應用於鑰匙交換方面(製作秘密鑰匙,再用它來加密),這與 RSA 演算法的使用有很大的區隔。
Diffie-Hellman 鑰匙交換法是利用 RSA 編碼演算法的特性(同餘乘法與指數運算),雙方互相傳送一段訊息,他們再由這些訊息建立共享鑰匙(又稱會議鑰匙)。其演算法敘述如下:首先 Alice 與 Bob 共用 n 與 g 兩個參數(n, g 是公開的,又稱公鑰),其中 n 是很大的質數且 g 是 n 的原根(primitive),並且 (n - 1) 必須有很大的質因數;接下來,Alice 與 Bob 各選擇一個小於 n 的數值 x 與 y (又稱私鑰),必須是秘密的,不可讓他人知道(經過運算後很難知道)。其運作程序如圖 3-5 所示,說明如下:
訊號 (1):Alice 選擇一個小於 n 的數值 x,計算 gx mod n,並將計算結果傳送給 Bob(該值又稱為『鑰匙材料』)。
訊號 (2):Bob 也選擇一個小於 n 的數值 y,同樣計算 gy mod n,並將計算結果(鑰匙材料)傳送給 Alice。
訊號 (3):Alice與Bob分別將收到的訊息(gy mod n)與(gx mod n),使用自己的私鑰分別計算(gy mod n)x 與(gx mod n)y,其結果都等於(gyx mod n),該數值便成為他們雙方共享的會議鑰匙。
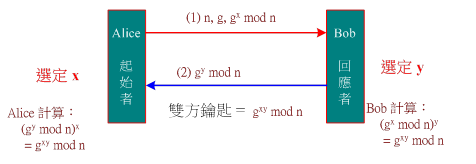
圖 3-5 Diffie-Hellman 鑰匙交換的運作程序
簡單的說,DH 演算法是利用:
(gx mod n)y mod n = (gy mod n) x mod = gxy mod n
同餘運算的特性來達成。我們先以一個例子說明,再討論其安全性。假設公開參數(公鑰)分別是 n = 47與g = 3(通訊雙方皆知曉),雙方建立會議鑰匙如下:
gx mod n = 38 mod 47 ≡ 28 mod 47
計算過程如下: 31 = 3 ≡ 3 mod 47 32≡ (3 × 3) mod 47 ≡ 9 mod 47 34≡ (9 × 9) mod 47 ≡ 81 mod 47 ≡ 34 mod 47 38≡ (34 × 34) mod 47 ≡ 1156 mod 47 ≡ 28 mod 47 |
則 Alice 傳送 {28}(鑰匙材料)給 Bob。
gy mod n = 310 mod 47 = 17 mod 47
計算過程如下: 31 = 3 ≡ 3 mod 47 32≡ (3 × 3) mod 47 ≡ 9 mod 47 34≡ (9 × 9) mod 47 ≡ 81 mod 47 ≡ 34 mod 47 38≡ (34 × 34) mod 47 ≡ 1156 mod 47 ≡ 28 mod 47 310 = 38× 32≡ (28 × 9) mod 47 ≡ 17 mod 47 |
則 Bob 傳送 {17} 給 Alice。同時 Bob 利用 Alice 傳送鑰匙材料 {28} 計算會議鑰匙,如下:(會議鑰匙 = 4)
(gx mod n)y = gxy mod n = 2810 mod 47 = 4 mod 47
計算過程如下: 281 = 28 ≡ 28 mod 47 282≡ (28 × 28) mod 47 ≡ 32 mod 47 283≡ (32 × 28) mod 47 ≡ 3 mod 47 2810≡ (3 × 3 × 3 × 28) mod 47 ≡ 4 mod 47 |
(gy mod n)x = gxy mod n = 178 mod 47 = 4 mod 47
計算過程如下: 171 = 17 ≡ 17 mod 47 172≡ (17 × 17) mod 47 ≡ 289 mod 47 ≡ 7 mod 47 174≡ (7 × 7) mod 47 ≡ 2 mod 47 178≡ (2 × 2 ) mod 47 ≡ 4 mod 47 |
最後我們可以發現,Alice與Bob所計算出來的值都是 4,該值就是他們的共享鑰匙。
雖然Diffie-Hellman 演算法要從公開參數(公鑰)計算出私鑰不容易,但可能遭受『中間人攻擊』(Man-in-the-middle Attack)。圖 3-6 中,假設 Alice 欲與 Bob 通訊:
訊號 (1):Alice送出交換鑰匙訊息(gx mod n)給 Bob,但此訊息被 Trudy 攔截到。
訊號 (2):當Trudy 知道訊息欲由 Alice 發送至 Bob ;便偽裝成 Alice,並發送交換鑰匙訊息(gz mod n)給 Bob。
訊號 (3):同時Trudy 亦偽裝Bob,回應鑰匙交換訊息(gz mod n)給 Alice,此時 Alice 與 Trudy 便建立了共享鑰匙(gxz mod n)。
訊號 (4):另一方面,Bob 收到 Trudy 的訊息之後,誤認為係由 Alice 傳送過來的,便回應鑰匙交換訊息(gy mod n)給 Trudy,並建立共享鑰匙(gzy mod n)。
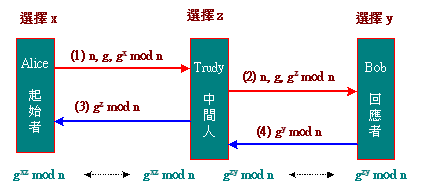
圖 3-6 中間人攻擊
接下來會發生什麼事情已不必多言,Alice 與 Bob 都誤認為 Trudy 是他們通訊的對象,他們之間通訊的訊息必然被Bob一覽無遺,一般我們又稱為『桶列攻擊法』(Bucket Bridge Attack)。
Diffie-Hellman 鑰匙交換法對資訊安全的貢獻非常大,其實中間人攻擊法並不難防禦,諸多文獻已提出解決方案,並且已嵌入許多安全系統中。接下來,介紹幾種防禦方法,這些方法或許會被混合使用(因為沒有一種方法是百分之一百安全的)。
【(A)公開 Diffie-Hellman 參數】
Diffie-Hellman 演算法中有兩個公開的參數 n 與 g,若將其值固定,並且對外公佈(由鑰匙交換協定規範)。當中間人攔截到訊息之後,因無法傳送另一個參數欺騙另一方(如圖 4-8 訊號 (2)),就可以避免中間人的主動攻擊,但儘管如此,也不盡然能完全防禦中間人攻擊,仍需仰賴其它配套措施。
【(B)認證的 Diffie-Hellman】
遭受中間人攻擊的主要原因,是因為不能確認通訊對方的身分,若能在交換訊息之前,先確認彼此身分,便不會受到攻擊,『認證的 Diffie-Hellman』(Authenticated Diffie-Hellman) 正是如此,其實現的方法有下列幾種:
利用『前置共享密鑰』(Pre-shared Secret)向 Diffie-Hellman 交換訊息加密。雙方先建立一個安全通道之後,再利用此安全通道交換訊息,一般又稱為兩階段的訊息交換(第十六與十七章再詳細介紹)。
利用對方的公開鑰匙向 Diffie-Hellman 交換訊息加密。
利用自己的私有鑰匙向 Diffie-Hellman 交換訊息加密。
在 Diffie-Hellman 交換之後,緊接著傳送 Diffie-Hellman 共享數值、名稱、與前置共享密鑰的雜湊值。
在 Diffie-Hellman 交換之後,緊接著傳送前置共享密鑰與所傳送 Diffie-Hellman 參數的雜湊值。
後面兩種方法,都能提供再確認的功能,至於如何建立安全通道之『前置共享密鑰』的方法,爾後再詳細介紹。
早期 Diffie-Hellman 提出公開鑰匙系統的概念時,所考慮的是如何解決網路文件認證的問題,就是所謂的『數位簽章』。公鑰密碼學經過幾年的發展之後,慢慢建立了公信力,其安全性已漸漸受到大眾的信賴。
使用公開鑰匙系統有兩件重要的現象必須特別注意:(1) 加密與解密的運算量非常龐大;(2) 公開鑰匙必須長時間的暴露。其中最重要的是第二個現象,攻擊者可嘗試利用公開鑰匙加密後的密文,來尋找出私有鑰匙;或者直接由私有鑰匙所加密的密文,找出私有鑰匙(採用選擇明文);最基本的方法即是利用暴力攻擊法。因此,勢必增加鑰匙長度才能延長暴力攻擊的破解時間,另一方面,也可以增加演算法複雜度來增加破解計算的時間。一般情況為了增加公開鑰匙的安全性,則利用私有鑰匙加密的訊息越短越安全;另一方面,雖然利用公開鑰匙加密的密文較不會有安全性的問題,但因運算量較大,並不利於大量資料的處理。由此可見,利用公開鑰匙系統也會有某些侷限的範圍,我們將它的主要功能歸類如下:
加密 / 解密:傳送者利用接收者的公開鑰匙加密;接收者再利用自己的私有鑰匙解密。以密碼學的觀點來講,此為提供傳輸資料的『隱密性』或『安全性』功能。但其計算量較大,對於大量資料加密或解密需要較長的編碼時間,因此較不適合於運用於隱密性傳輸,一般較常使用於『會議鑰匙』或『秘密鑰匙』等較短資料傳輸上。
數位簽章:傳送者利用自己的私有鑰匙加密,接收者再利用傳送者的公開鑰匙來解密,以密碼學的觀點來講,是提供傳輸資料的『確認性』。至於如何產生數位簽章的訊息,我們在第七章有更詳細的介紹。
鑰匙交換:通訊雙方利用公鑰密碼演算法,可共同製造一把秘密分享的『會議鑰匙』。
圖 3-7 主要說明上述前面兩項的功能。假設發送端(A)與接收端(B)分別擁有一對鑰匙 {KUa, KRa} 與 {KUb, KRb},並且雙方彼此知道對方的公開鑰匙(KUa與 KUb)。隱密性傳輸功能如圖 4-2 (a) 所示,發送端用接收端的公開鑰匙(KUb)向資料加密,接收端再用自己的私有鑰匙(KRb)解密,盜取者因沒有接收端的私有鑰匙,所以無法觀察出資料的內容。
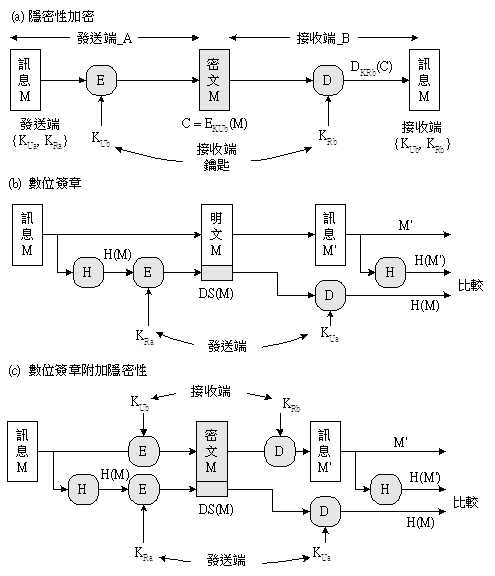
圖 3-7 公開鑰匙系統的功能
圖 3-7 (b) 為數位簽章功能。發送者將訊息經過雜湊函數(第五章介紹)計算後,得到一個雜湊碼,再利用自己的私有鑰匙(KRa)加密,同時將加密後的簽章碼附加於訊息後面一起傳送給接收端,接收端收到訊息後,利用同樣的雜湊函數計算出另一個雜湊碼,同時也利用對方的公開鑰匙(KUa)向所收到的簽章碼解密,便可得到對方所送的雜湊碼。如果兩者相同的話,表示訊息的確是由發送端所傳送,且未遭受竄改,如此便是確認性功能。圖 3-7 (c) 為數位簽章附加隱密性功能,表示訊息傳輸之前先利用接收端的公開鑰匙(KUb)加密,所以唯有接收端的私有鑰匙(KRb)才可以解密,如此便可以增加隱密性的功能。當然還有許多運作方式,本書將會陸續介紹到。